Artykuły

Programowanie sieciowe

Programowanie sieciowe to przedstawienie problemu w postaci grafu, a następnie analizowanie takiego grafu przy zastosowaniu teorii grafów.

Programowanie sieciowe wykorzystywane jest przy planowaniu, harmonogramowaniu i kontroli realizacji przedsięwzięć (metody CPM i PERT, diagram Gantta). Programowanie sieciowe pomaga w identyfikacji odstępstw od planu i ich skutków, modyfikacjach harmonogramu.

Żródło: https://pl.wikipedia.org/wiki/Programowanie_sieciowe

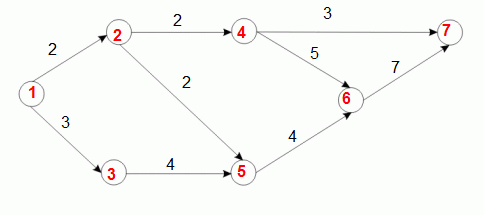
Weźmy przykładowy graf: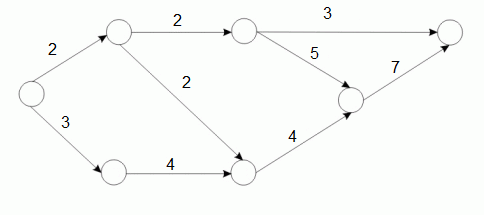

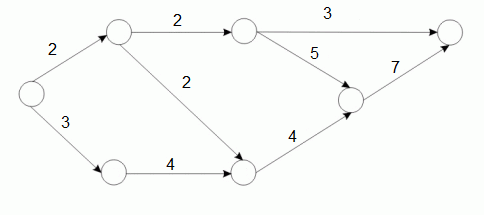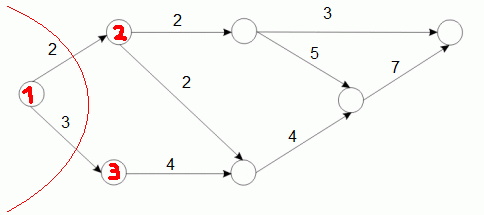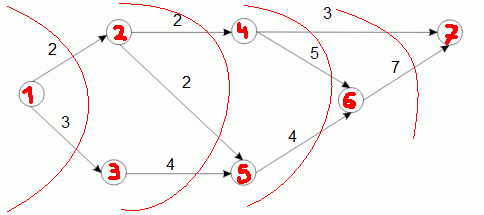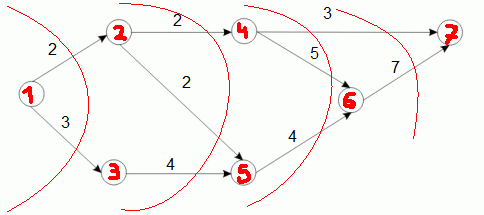
Jeszcze przed zajmowaniem się nim powinniśmy upewnić się, że graf ma dokładnie jeden wierzchołek początkowy i jeden końcowy. W tym przypadku tak jest, jeśli jednak takich wierzchołków byłoby więcej, np. mielibyśmy dwa wierzchołki początkowe, należałoby dodać sztucznie utworzony wierzchołek oraz łuki łączące ten nowy wierzchołek z każdym wierzchołkiem startowym. Łuki te należy dodać z wartością 0.

Pierwszą czynnością, jaką powinniśmy wykonać jest ponumerowanie wierzchołków. Robimy to zaczynając od wierzchołków, które nie posiadają łuków wchodzących. Numerujemy je w dowolnej kolejności, po czym zapominamy o nich oraz o łukach wychodzących z nich. W kolejnych iteracjach powtarzamy numerowanie do czasu gdy ponumerujemy już wszystkie wierzchołki. Proces numerowania przedstawia poniższa grafika (wierzchołkami i łukami po lewej stronie od czerwonej linii się nie zajmujemy):

Ostateczne ponumerowanie:

Teraz zajmiemy się wyznaczaniem ścieżki krytycznej - czyli dla każdego zdarzenia będziemy szukać najwcześniejszego momentu jego wystąpienia. Tutaj nie ma żadnej filozofii, wystarczy zapamiętać prostą regułę. Po pierwsze przechodzimy po wszystkich wierzchołkach zgodnie z nadanymi im wcześniej numerami (no bo po coś je chyba nadawiliśmy). Dla każdego wierzchołka najwcześniejszy moment wystąpienia zdarzenia (czyli ta cyferka, którą chcemy teraz obliczyć) to po prostu maksymalna suma wag łuków wchodzących do danego wierzchołka i najwcześniejszego momentu wystąpienia zdarzenia przy wyjściach tych łuków. Prościej: sumujemy wartości na łukach i poprzedzających je wierzchołkach, następnie wybieramy wartość największą i tę wpisujemy jako najwcześniejszy moment wystąpienia zdarzenia.

Obliczanie najpóźniejszych momentów wystąpienia zdarzeń.

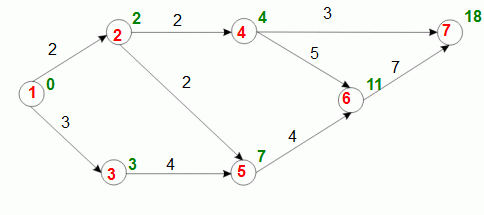
Najpóźniejszy moment wystąpienia zdarzenia to najpóźniejszy moment, w którym może zakończyć się zdarzenie przy założeniu, że całkowity czas projektu nie ulegnie zmianie. Liczy się go w zasadzie odwrotnie do tego jak się liczy najwcześniejszy moment wystąpienia zdarzenia. Przechodzimy przez wszystkie wierzchołki od ostatniego do pierwszego i poszukujemy minimalnej różnicy wartości w danym wierzchołku i łuków wchodzących do niego.
Aha, pierwsza wartość (przy wierzchołku końcowym) tego parametru jest zawsze równa czasowi wykonania całego projektu.

Wartości dla naszego przykładowego grafu przedstawia poniższa grafika:

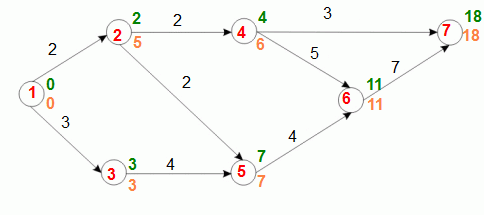
Na tym etapie już możemy coś powiedzieć o projekcie. Po pierwsze ścieżka krytyczna to taka ścieżka, której wierzchołki obie wartości - zieloną i pomarańczową (lub jak kto woli #008000 i #FF8040) mają równe. Różnica tych wartości nazywana jest "luzem" i określa czas, o jaki mogłoby się opóźnić dane zdarzenie bez wydłużenia czasu realizacji całości projektu.

Pozostaje jeszcze obliczenie zapasów całkowitych czynności czyli czasu, o jaki można wydłużyć daną czynność, aby cały projekt się nie wydłużył. Nie chce mi się rysować graficzek, więc podam na szybcika, że dla każdego łuku (tak, tym razem liczymy wartości dla łuków) bierzemy pomarańczową wartość przy wyjściu z łuku i od niej odejmujemy wartość na łuku oraz zieloną wartość przy wejściu łuku. Przykładowo dła łuku między wierzchołkami 2 i 4 szukana wartość to 6 - 2 - 2 = 2, zatem zapas dla tej czynności wynosi 2. Możecie zatem podczas tej czynności opierdzielać się przez 2 jednostki czasu i nie wpłynie to na długość wykonania całego projektu.

Łuki z zerowym zapasem leżą na ścieżce krytycznej i nie wolno ich wydłużać, jeśli nie chcemy wydłużyć czasu wykonania całego projektu.

PS: Nie, nie dam wam namiarów na mojego dilera.

Na górę