Artykuły

Aktualizacja asynchroniczna w sieci Hopfielda

Przeanalizuję tutaj przykład ze slajdu dr. inż. A. Michalskiego - strona 37. w tym dokumencie: www.cs.put.poznan.pl/amichalski/wsi/AI8.ann.b&w.pdf.

Oto owy przykład:

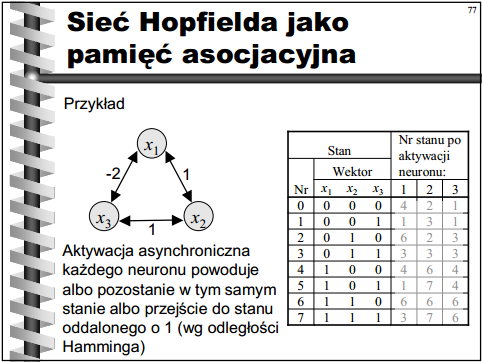
Naszym zadaniem jest określenie, jak zachowa się układ neuronów po każdej możliwej zmianie w sieci (rozwiązanie zostało przedstawione w szarej części tabeli). Mamy 8 możliwych stanów początkowych oraz 3 neurony, które mogą zostać aktywowane, zatem możliwych zmian w tej sieci jest 21. Aby wypełnić tabelkę wystarczy zastosować jeden "magiczny" wzór (w dokumencie na str. 33) do każdego pola z osobna:

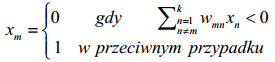, gdzie:
X_m - stan aktywowanego neuronu po aktywacji
m - numer aktywowanego neuronu
k - liczba wszystkich neuronów
w_mn - wartość krawędzi między neuronami m i n
x_n - stan neuronu n (0 lub 1)

Najprościej mówiąc liczymy sumę wartości krawędzi (na grafie) łączących neuron aktywowany ze wszystkimi innymi neuronami o stanie 1. Gdy uzyskamy wartość ujemną, stan neuronu ustalamy na 0, w przeciwnym wypadku 1. Warto zapamiętać, że wartość 0 wystarcza na "zapalenie" neuronu.

Uwzględniając właśnie obliczoną wartość dla aktywowanego neuronu, zapisujemy zaktualizowany stan sieci w odpowiednim polu.

To właściwie cała teoria w tej kwestii, reszta to tylko zrozumienie zadania i zastosowanie się do poleceń. Należy pamiętać, że stan całej sieci to stan wszystkich neuronów. Zatem jeśli chcemy zapisać stan systemu (1, 1, 0) w odpowiednie pole w tabeli wpisujemy 6.

Na slajdzie jest napisana ważna informacja - po aktywacji pojedynczego neuronu stan całego systemu może zmienić się co najwyżej o jeden bit (np. z 6 na 2) - i jest to bit przyporządkowany aktywowanemu neuronowi.

Aby wszystko było jasne, rozważymy ostatnie pole tabeli - czyli przy stanie sieci (1, 1, 1) aktywujemy neuron x3.

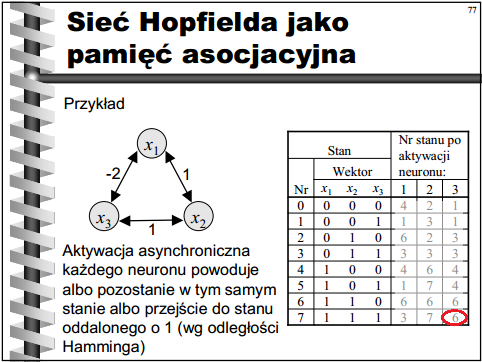
Neurony x1 oraz x2 mają wartość 1, więc bierzemy je oba pod uwagę. Liczymy sumę: w_x3x1 + w_x3x2 = -2 + 1 = -1. Suma jest ujemna, czyli neuron przyjmuje wartość 0. Nowy stan systemu to (1, 1, 0), zatem do tabelki wpisujemy wartość 6. Warto zauważyć, że jest to stan stabilny, gdyż nie ma możliwości aktywacji neuronu w taki sposób, aby go zmienić (ale do tego wniosku możemy dojść dopiero po wypełnieniu całego wiersza tabelki).

Na górę